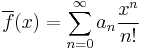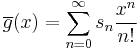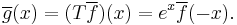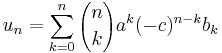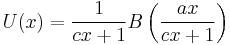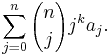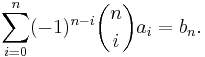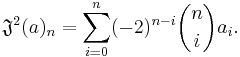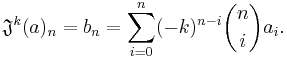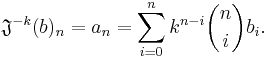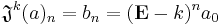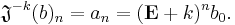Binomial transform
In combinatorics, the binomial transform is a sequence transformation (i.e., a transform of a sequence) that computes its forward differences. It is closely related to the Euler transform, which is the result of applying the binomial transform to the sequence associated with its ordinary generating function.
Contents |
Definition
The binomial transform, T, of a sequence, 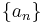 , is the sequence
, is the sequence 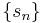 defined by
defined by
Formally, one may write 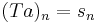 for the transformation, where T is an infinite-dimensional operator with matrix elements
for the transformation, where T is an infinite-dimensional operator with matrix elements 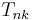 :
:
The transform is an involution, that is,
or, using index notation,
where δ is the Kronecker delta function. The original series can be regained by
The binomial transform of a sequence is just the nth forward difference of the sequence, with odd differences carrying a negative sign, namely:
where Δ is the forward difference operator.
Some authors define the binomial transform with an extra sign, so that it is not self-inverse:
whose inverse is
Example
Binomial transforms can be seen in difference tables. Consider the following:
| 0 | 1 | 10 | 63 | 324 | 1485 | |||||
| 1 | 9 | 53 | 261 | 1161 | ||||||
| 8 | 44 | 208 | 900 | |||||||
| 36 | 164 | 692 | ||||||||
| 128 | 528 | |||||||||
| 400 |
The top line 0, 1, 10, 63, 324, 1485,... (a sequence defined by 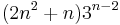 ) is the binomial transform of the diagonal 0, 1, 8, 36, 128, 400,... (a sequence defined by
) is the binomial transform of the diagonal 0, 1, 8, 36, 128, 400,... (a sequence defined by 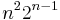 ).
).
Shift states
The binomial transform is the shift operator for the Bell numbers. That is,
where the 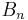 are the Bell numbers.
are the Bell numbers.
Ordinary generating function
The transform connects the generating functions associated with the series. For the ordinary generating function, let
and
then
Euler transform
The relationship between the ordinary generating functions is sometimes called the Euler transform. It commonly makes its appearance in one of two different ways. In one form, it is used to accelerate the convergence of an alternating series. That is, one has the identity
which is obtained by substituting x=1/2 into the last formula above. The terms on the right hand side typically become much smaller, much more rapidly, thus allowing rapid numerical summation.
The Euler transform can be generalized (Borisov B. and Shkodrov V., 2007):
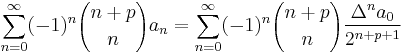 ,
,
where p = 0, 1, 2,...
The Euler transform is also frequently applied to the Euler hypergeometric integral 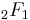 . Here, the Euler transform takes the form:
. Here, the Euler transform takes the form:
The binomial transform, and its variation as the Euler transform, is notable for its connection to the continued fraction representation of a number. Let 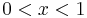 have the continued fraction representation
have the continued fraction representation
then
and
Exponential generating function
For the exponential generating function, let
and
then
The Borel transform will convert the ordinary generating function to the exponential generating function.
Integral representation
When the sequence can be interpolated by a complex analytic function, then the binomial transform of the sequence can be represented by means of a Nörlund–Rice integral on the interpolating function.
Generalizations
Prodinger gives a related, modular-like transformation: letting
gives
where U and B are the ordinary generating functions associated with the series 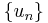 and
and 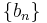 , respectively.
, respectively.
The rising k-binomial transform is sometimes defined as
The falling k-binomial transform is
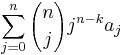 .
.
Both are homomorphisms of the kernel of the Hankel transform of a series.
In the case where the binomial transform is defined as
Let this be equal to the function 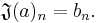
If a new forward difference table is made and the first elements from each row of this table are taken to form a new sequence 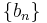 , then the second binomial transform of the original sequence is,
, then the second binomial transform of the original sequence is,
If the same process is repeated k times, then it follows that,
Its inverse is,
This can be generalized as,
where 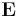 is the shift operator.
is the shift operator.
Its inverse is
See also
- Newton series
- Hankel matrix
- Möbius transform
- Stirling transform
- Euler summation
- List of factorial and binomial topics
References
- John H. Conway and Richard K. Guy, 1996, The Book of Numbers
- Donald E. Knuth, The Art of Computer Programming Vol. 3, (1973) Addison-Wesley, Reading, MA.
- Helmut Prodinger, 1992, Some information about the Binomial transform
- Michael Z. Spivey and Laura L. Steil, 2006, The k-Binomial Transforms and the Hankel Transform
- Borisov B. and Shkodrov V., 2007, Divergent Series in the Generalized Binomial Transform, Adv. Stud. Cont. Math., 14 (1): 77-82
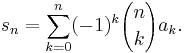
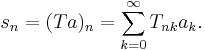
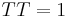
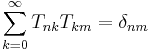
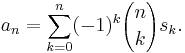
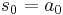
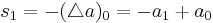
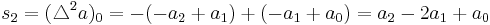

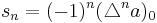
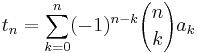
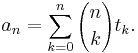
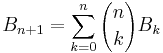
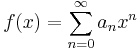
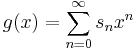
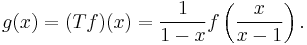
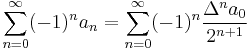
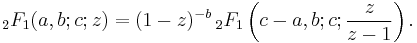
![x=[0;a_1, a_2, a_3,\cdots]](/2012-wikipedia_en_all_nopic_01_2012/I/5bade4280d3a9f547e620492527584ca.png)
![\frac{x}{1-x}=[0;a_1-1, a_2, a_3,\cdots]](/2012-wikipedia_en_all_nopic_01_2012/I/77d54d68045c9eedeb2cab19b382af3f.png)
![\frac{x}{1%2Bx}=[0;a_1%2B1, a_2, a_3,\cdots].](/2012-wikipedia_en_all_nopic_01_2012/I/cab00a6565836049818a1ca439387ccc.png)